Konvexné polygóny. Definícia konvexného mnohouholníka. Diagonály konvexného mnohouholníka

Tieto geometrické postavy nás obklopujú všade. Vypuklého mnohouholníka sú prírodné, ako je napríklad včelieho plástu alebo umelé (umelých). Tieto čísla sa používajú pri výrobe rôznych typov náterov, v maľovaní, architektúre, dekoráciách atď. Konvexné polygóny majú vlastnosť, že všetky ich body sú umiestnené na jednej strane čiary, ktorá prechádza cez pár susedných vrcholov tejto geometrickej postavy. Existujú aj iné definície. Konvexný je ten polygón, ktorý je umiestnený v jednej polovičnej rovine vzhľadom na ľubovoľnú čiaru obsahujúcu jednu zo svojich strán.

Konvexné polygóny

V priebehu elementárnej geometrie vždypovažujeme len za jednoduché polygóny. Aby sme pochopili všetky vlastnosti takých geometrických útvarov, je potrebné porozumieť ich charakteru. Najprv treba chápať, že akékoľvek čiary, ktorých konce sa zhodujú, sa nazývajú uzavreté. A postavu, ktorú tvorí, môže mať rôzne konfigurácie. Polygón je jednoduchá uzavretá polygonálna čiara, ktorej susedné väzby nie sú na tej istej línii. Jeho väzby a vrcholy predstavujú strany a vrcholy tejto geometrickej postavy. Jednoduchá krivka nesmie mať seba-križovatky.

Vrcholy mnohouholníka sa nazývajú v susedstveak predstavujú konce jednej zo strán. Geometrická figurka, ktorá má n-tý počet vrcholov, a teda aj n-tý počet strán, sa nazýva n-gon. Prerušovaná čiara sa nazýva hranica alebo obrys tejto geometrickej postavy. Viacúrovňová rovina alebo rovinný polygón sa nazýva konečnou časťou akejkoľvek roviny, ktorá je ohraničená. Susedné strany tejto geometrickej postavy sú segmenty prerušovanej čiary začínajúcej od jedného vrcholu. Nebudú susedia, ak pochádzajú z rôznych vrcholov polygónu.

Ďalšie definície konvexných polygónov

V základnej geometrii existuje niekoľko ďalšíchekvivalent v zmysle definícií, čo naznačuje, ktorý polygón sa nazýva konvexný. A všetky tieto formulácie sú rovnako pravdivé. Konvexný polygón sa považuje za:

• každý segment, ktorý spája akékoľvek dva body vo vnútri, je v ňom úplne;

• vnútri ležia všetky jeho diagonály;

• akýkoľvek vnútorný uhol nepresahuje 180 °.

Viacúhelník vždy rozdeľuje rovinu o 2part. Jedna z nich je obmedzená (môže byť uzavretá v kruhu) a druhá je neobmedzená. Prvá sa nazýva vnútorná oblasť a druhá sa nazýva vonkajšia oblasť tejto geometrickej postavy. Tento polygón je križovatka (inými slovami - spoločná zložka) niekoľkých poloplánov. V tomto prípade každý segment, ktorý končí v bodoch, ktoré patria k polygónu, úplne patrí tomuto.

Variety konvexných mnohouholníkov

Definícia konvexného mnohouholníka nenaznačujena skutočnosť, že existuje veľa druhov. A každý z nich má určité kritériá. To znamená, že konvexný mnohouholníky, ktoré majú vnútorný uhol 180 °, uvedené mierne konvexné. Konvexné geometrického obrazca, ktorý má tri vrcholy, sa nazýva trojuholník, štyri - štvoruholník, päť - päťuholník, atď Každý konvexné n-gons spĺňa nasledujúce dôležité požiadavky: .. N musí byť rovná alebo väčšia ako 3. Každá z týchto trojuholníkov je konvexný. Geometrická postava tohto typu, v ktorom sú všetky vrcholy ležia na kružnici, sa nazýva vpísanou kružnici. Konvexný polygón sa nazýva opísaný, ak sa ho dotýkajú všetky jeho strany v blízkosti kruhu. Dva polygóny sa nazývajú rovnať iba v prípade, že pri použití prekrytia možné kombinovať. Ploché polygón tzv polygonálne rovina (rovina časť), ktorý tejto obmedzenej geometrický obrazec.

Pravidelné konvexné polygóny

Správne polygóny sú volanégeometrické obrázky s rovnakými uhlami a stranami. Vo vnútri je bod 0, ktorý je v rovnakej vzdialenosti od každého z jeho vrcholov. Nazýva sa stredom tejto geometrickej postavy. Segmenty, ktoré spájajú stred s vrcholmi tejto geometrickej postavy, sa nazývajú apofémy a tie, ktoré spájajú bod 0 so stranami, sú polomery.

Pravý štvoruholník je štvorec. Pravý trojuholník sa nazýva rovnostranný. Pre takéto čísla existuje nasledovné pravidlo: každý uhol konvexného mnohouholníka je 180 ° * (n-2) / n,

kde n je počet vrcholov tejto konvexnej geometrickej postavy.

Oblasť ľubovoľného pravidelného polygónu je definovaná vzorcom:

S = p * h,

kde p sa rovná polovici súčtu všetkých strán daného polygónu a h sa rovná dĺžke apophema.

Vlastnosti konvexných polygónov

Konvexné polygóny majú určité vlastnosti. Takže segment, ktorý spája akékoľvek dva body takejto geometrickej postavy, je nevyhnutne umiestnený v nej. dôkaz:

Predpokladajme, že P je daná konvexnápolygón. Vezmite dva ľubovoľné body, napríklad A a B, ktoré patria do P. Podľa súčasnej definície konvexný polygón, tieto body sú umiestnené na jednej strane priamky, ktorá obsahuje ľubovoľnom smere R. V dôsledku toho, AB má rovnako túto vlastnosť a je obsiahnutý v R. A konvexný polygón vždy môže byť rozdelená do niekoľkých trojuholníkov úplne všetky uhlopriečky, ktorá sa konala jeden zo svojich vrcholov.

Úhly konvexných geometrických tvarov

Úhly konvexného mnohouholníka sú úhlysú tvorené jej stranami. Vnútorné rohy sú vo vnútornej oblasti tohto geometrického obrázku. Uhol, ktorý je tvorený jeho stranami, ktoré sa zbiehajú na jednom vrchole, sa nazýva uhol konvexného mnohouholníka. Uhol priliehajúci k vnútorným uhlov daného geometrického tvaru sa nazýva vonkajšie. Každý uhol konvexného mnohouholníka, ktorý sa nachádza vo vnútri, sa rovná:

180 ° - x,

kde x je hodnota vonkajšieho uhla. Tento jednoduchý vzorec platí pre všetky geometrické obrázky tohto typu.

Vo všeobecnom prípade existujú vonkajšie uhlynasledujúce pravidlo: každý uhol konvexného mnohouholníka sa rovná rozdielu medzi 180 ° a hodnotou vnútorného uhla. Môže mať hodnoty v rozmedzí -180 ° až 180 °. Preto keď je vnútorný uhol 120 °, vonkajší uhol bude 60 °.

Súčet uhlov konvexných polygónov

Súčet vnútorných uhlov konvexného mnohouholníka je stanovený vzorcom:

180 ° * (n-2),

kde n je počet vrcholov n-gonu.

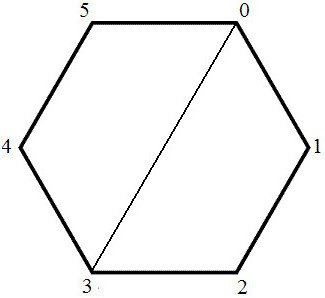
Súčet uhlov konvexného mnohouholníka sa vypočítajednoducho. Uvažujme o takomto geometrickom obrázku. Ak chcete zistiť súčet uhlov v konvexnom polygóne je potrebné pripojiť jeden zo svojich vrcholov s ostatnými vrcholmi. V dôsledku tejto akcie získavame (n-2) trojuholníky. Je známe, že súčet uhlov akéhokoľvek trojuholníka je vždy 180 °. Vzhľadom k tomu, ich počet v každom polygónu rovná (n-2), pričom súčet vnútorných uhlov na obrázku je 180 ° x (n-2).

Súčet uhlov konvexného mnohouholníka, tj.ktorékoľvek dve susedné vnútorné a vonkajšie uhly na ne, v tomto konvexného geometrického útvaru bude vždy rovný 180 °. Na tomto základe môžeme určiť súčet všetkých jej rohov:

180 x n.

Súčet vnútorných uhlov je 180 ° * (n-2). Vychádzajúc z toho súčet všetkých vonkajších uhlov daného čísla je stanovený vzorcom:

180 ° * n-180 ° - (n-2) = 360 °.

Súčet vonkajších uhlov každého konvexného mnohouholníka bude vždy 360 ° (bez ohľadu na počet jeho strán).

Vonkajší uhol konvexného mnohouholníka je všeobecne reprezentovaný rozdielom medzi 180 ° a hodnotou vnútorného uhla.

Ďalšie vlastnosti konvexného mnohouholníka

Okrem základných vlastností týchto geometrickýchčísla, majú iné, ktoré vznikajú pri ich manipulácii. Takže každý z polygónov môže byť rozdelený na niekoľko konvexných n-gónov. Za týmto účelom je potrebné pokračovať v každej strane a rozrezať túto geometrickú figúrku pozdĺž týchto priamok. Rozdelte ľubovoľný polygón na niekoľko konvexných častí a takým spôsobom, že vrcholy každého kusa sa zhodujú so všetkými jeho vrcholmi. Z tohto geometrického obrázku je veľmi jednoduché vytvoriť trojuholníky tým, že držíte všetky diagonály z jedného vrcholu. Takže každý polygon v konečnom dôsledku môže byť rozdelený na určitý počet trojuholníkov, čo je veľmi užitočné pri riešení rôznych problémov spojených s takými geometrickými číslami.

Obvod konvexného mnohouholníka

Časti křivky nazývané stranypolygon, najčastejšie označovaný nasledujúcimi písmenami: ab, bc, cd, de, ea. Toto sú strany geometrického tvaru s vrcholmi a, b, c, d, e. Súčet dĺžok všetkých strán tohto konvexného mnohouholníka sa nazýva jeho obvod.

Kruh polygónu

Môžu byť napísané konvexné polygóny aopísané. Kruh dotýkajúci sa všetkých strán tejto geometrickej postavy sa nazýva do nej zapísaný. Takýto polygón sa nazýva opísaný. Stred kruhu, ktorý je napísaný v polygóne, je priesečník priesečníkov všetkých uhlov v rámci daného geometrického obrázku. Plocha takéhoto polygónu sa rovná:

S = p * r,

kde r je polomer zapísaného kruhu a p je semiperimeter daného polygónu.

Kruh obsahujúci vrcholy mnohouholníka,nazývaný v jeho blízkosti. V tomto prípade sa táto konvexná geometrická postava nazýva napísaná. Stred kruhu, ktorý je popísaný v blízkosti takého polygónu, predstavuje priesečník takzvaných stredných kolíkov všetkých strán.

Diagonály konvexných geometrických tvarov

Diagonály konvexného mnohouholníka sú segmenty,ktorý spája nie susedné vrcholy. Každý z nich leží v tejto geometrickej osobe. Počet uhlopriečok takéhoto n-gonu je stanovený vzorcom:

N = n (n-3) / 2.

Zobrazí sa počet uhlopriečok konvexného polygónudôležitú úlohu v elementárnej geometrii. Počet trojuholníkov (K), do ktorých možno rozdeliť každý konvexný polygón, sa vypočíta podľa tohto vzorca:

K = n - 2.

Počet uhlopriečok konvexného mnohouholníka vždy závisí od počtu jeho vrcholov.

Rozdelenie konvexného mnohouholníka

V niektorých prípadoch riešiť geometrickéje potrebné rozdeliť konvexný mnohouholník na niekoľko trojuholníkov s rozloženými diagonálmi. Tento problém možno vyriešiť odvodením definitívneho vzorca.

Definovanie problému: volanie správny druh rozdelenie konvexný n-gon do niekoľkých trojuholníky uhlopriečok, ktoré sa pretínajú len na vrcholoch geometrického útvaru.

riešenie: Predpokladajme, že P1, P2, P3 ..., Pn sú vrcholy tohto n-gonu. Číslo Xn je počet jeho oddielov. Pozorne uvažujeme výslednú uhlopriečku geometrického tvaru Pi Pn. V ktorejkoľvek z bežných oddielov P1 Pn patrí do určitého trojuholníka P1 Pi Pn, pre ktorý 1 <i <n. Vychádzajúc z tohto a za predpokladu, že i = 2,3,4 ..., n-1, sme získali (n-2) skupiny týchto oddielov, do ktorých sú zahrnuté všetky možné špeciálne prípady.

Nech je i = 2 jedna pravidelná skupinaktorý vždy obsahuje diagonálnu P2 Pn. Počet oddielov, ktoré vstupujú do nej, sa zhoduje s počtom oddielov (n-1) -gon P2 P3 P4 ... Pn. Inými slovami, to sa rovná Xn-1.

Ak i = 3, potom bude táto ďalšia skupina oddielovVždy obsahujú diagonálne P3 P1 a P3 PN. Počet správnych oddiely, ktoré sú obsiahnuté v skupine, bude zhodovať s počtom oddielov (n-2) gon P3, P4, ... Pn. Inými slovami, bude Xn-2.

Nech je i = 4, potom medzi trojuholníky pravidelnérozklad bude nevyhnutne obsahovať trojuholník P1P4Pn, ku ktorému bude priliehať štvoruholník P1 P2P3P4, (n-3) -gon P4P5 ... Pn. Počet pravidelných oddielov takéhoto štvoruholníka sa rovná X4 a počet oddielov (n-3) -gon sa rovná Xn-3. Na základe vyššie uvedeného môžeme povedať, že celkový počet bežných oblastí, ktoré sú obsiahnuté v tejto skupine, je Xn-3 X4. Ostatné skupiny, pre ktoré i = 4, 5, 6, 7 ... budú obsahovať Xn-4 X5, Xn-5 X6, Xn-6 X7 ... bežných oddielov.

Nech je i = n-2, potom počet bežných oddielov v danej skupine sa zhoduje s počtom oddielov v skupine, pre ktoré i = 2 (inými slovami sa rovná Xn-1).

Keďže X1 = X2 = 0, X3 = 1, X4 = 2 ..., potom počet všetkých oddielov konvexného polygónu sa rovná:

Xn = Xn-1 + Xn-2 + Xn-3 X4 + Xn-4 X5 + ... + X5 Xn-4 + X4Xn-3 + Xn-2 + Xn-1.

príklad:

X5 = X4 + X3 + X4 = 5

X6 = X5 + X4 + X4 + X5 = 14

X7 = X6 + X5 + X4 * X4 + X5 + X6 = 42

X8 = X7 + X6 + X5 * X4 + X4 * X5 + X6 + X7 = 132

Počet bežných oblastí, ktoré pretínajú jednu uhlopriečku

Pri overovaní jednotlivých prípadov sa dá predpokladať, že počet uhlopriečok konvexných n-gónov sa rovná súčinu všetkých oddielov tohto čísla pomocou (n-3).

Dôkaz tohto predpokladu: Predstavme si, že P1N = Xn * (n-3), zatiaľ čo všetky n-gon môže byť rozdelený do (n-2) je trojuholník. Súčasne je možné kombinovať jeden z nich (n-3) - kvadrangle. Spolu s tým bude každý štvoruholník mať uhlopriečku. Od tohto konvexného geometrického útvaru dve diagonály sa môže vykonávať, čo znamená, že v žiadnej (n-3) -chetyrehugolnikah môžu vykonávať ďalšie diagonálny (n-3). Na tomto základe môžeme konštatovať, že v každom správnom oddiel má možnosť (n-3) -diagonali spĺňa požiadavky tejto úlohy.

Oblasť konvexných polygónov

Často pri riešení rôznych problémov, elementárnegeometria bude treba určiť oblasť konvexný polygón. Predpokladajme, že (XI. Yi), i = 1,2,3 ... n predstavuje postupnosť súradníc všetkých susedných vrcholov mnohouholníka, s nedochádza k samovoľnému križovatky. V tomto prípade sa jeho plocha vypočíta podľa tohto vzorca:

S = 1 (Σ (X_ja + X_{i + 1}) (Y_ja + Y_{i + 1})),

kde (X₁, Y₁) = (X_{n +1}, Y_{n + 1}).

</ p>